Bulgarian solitaire

In mathematics and game theory, Bulgarian solitaire is a random card game.

In the game, a pack of $N$ cards is divided into several piles. Then for each pile, either leave it intact or, with a fixed probability $p$ , remove one card; collect the removed cards together to form a new pile (piles of zero size are ignored).

If 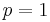$p=1$ , the game is known as Bulgarian solitaire or deterministic Bulgarian solitaire and was introduced by Martin Gardner; the general case with 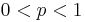$0<p<1$ is known as random Bulgarian solitaire or stochastic Bulgarian solitaire. This is a finite irreducible Markov chain.

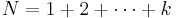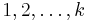If $N$ is a triangular number (that is, $N=1%2B2%2B\cdots%2Bk$ for some $k$ ), then it is known that deterministic Bulgarian solitaire will reach a stable configuration in which the sizes of the piles are $1,2,\ldots, k$ . This state is reached in 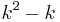$k^2-k$ moves or fewer. If $N$ is not triangular, no stable configuration exists and a limit cycle is reached.

In 2004, Brazilian probabilist of Russian origin Serguei Popov showed that stochastic Bulgarian solitaire spends "most" of its time in a "roughly" triangular distribution.

References

Serguei Popov (2005). "Random Bulgarian solitaire". Random Structures and Algorithms 27 (3): 310–330. doi:10.1002/rsa.20076.
Ethan Akin and Morton Davis (1985). "Bulgarian solitaire". American Mathematical Monthly 92 (4): 237–250. doi:10.2307/2323643. JSTOR 2323643.